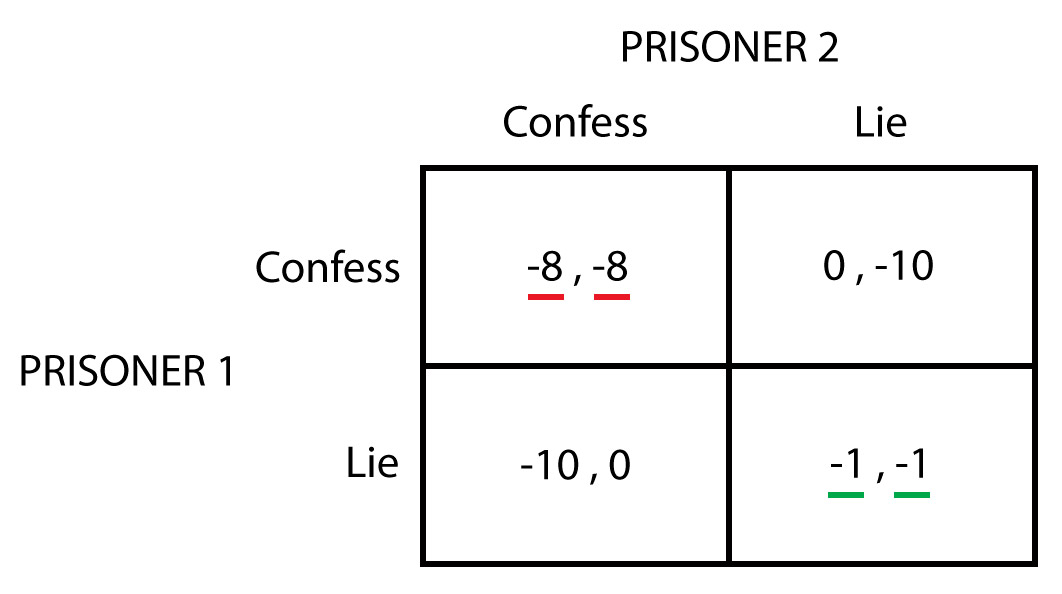
According to game theory, the dominant strategy is the optimal move for an individual regardless of how other players act. A Nash equilibrium describes the optimal state of the game where both players make optimal moves but now consider the moves of their opponent.
What is Nash Equilibrium Dominant Strategy?
Nash Equilibrium Dominant Strategy is a very important concept in the field of game theory and is used widely. Let us discuss different types of Nash Equilibrium Dominant Strategy:
Expressive Nash Equilibrium Dominant Strategy
It is a type of equilibrium that appears in a given situation that an individual player has a desire or motive to communicate or express its intent. In this type of Nash Equilibrium Dominant Strategy, a player is revealing to that other player that he has a reason for making a certain move.
Motiveless Nash Equilibrium Dominant Strategy
It is a type of equilibrium in which the players and their moves are independent of each other. In this type of Nash Equilibrium Dominant Strategy, the moves made by the players hold no importance to the others. This is mostly used in situations where the opponents are indifferent to each other and do not have any special relationship.
Uniform Nash Equilibrium Dominant Strategy
This will occur when the choices or options offered to the player are the same. One prime example is in universities and colleges where applicants are assigned a seat to qualify for admission based on their ranks in entrance tests.
Causal Nash Equilibrium Dominant Strategy
In this, the choice that is being made is determined by the cause or effect. It is a bit tough to understand in the beginning but it will make sense once we know the two types of Cone Dominant Strategy.
First Type of Causal Nash Equilibrium Dominant Strategy:
As the name suggests, in this type of Nash Equilibrium Dominant Strategy, the choice that is made is based on the cause and the choice that is made is dependent on previous choices.
For example, in a game of life, if the player is a smoker, then the chance of him passing out from smoking is high. In this situation, the smoker might decide to not smoke.
Second Type of Causal Nash Equilibrium Dominant Strategy:
In this type of Nash Equilibrium Dominant Strategy, the choice that is made is based on the cause and the choice that is made is dependent on the previous choice. For example, if the player is a smoker and is playing a lung cancer game, then the chance of him passing out of smoking is high. In this case, it is very likely that the player will not smoke at all.
Nash Equilibrium Dominant Strategy in Bookmaking
In this game, every player has to choose the probability for every possible event in the game. The goal is to pick a probability distribution that will maximize the payout to the player.
Let us take an example to make it more clear:
Suppose, there are three players A, B, and C. Here, player A has to choose the probability of Head. Let us assume that the possible combinations are: A = 6, P(A) = 1/3, and P(A) = 2/3. Hence, the payoff to A will be P(A) * 1. Odds also have to be chosen by each player and this is decided by the bookmaker beforehand. Hence, in this case, the possible payoff to A will be:
Hence, A will want to choose P(A) = 1/3 and the bookmaker will chose P(A) to be 1/3 and the payoff to player A will be 30. Thus, Nash Equilibrium Dominant Strategy will be when P(A) is set to 1/3.
From the above example, A will get $40 when he selects this option. The payoff to player B and C will be: B = 10 and C = -10. Hence, they will select P(B) and P(C) to be 2/3.
Let us now see what happens when P(A) is set to be 2/3.
When P(A) is set to be 2/3, the roles of players A, B, and C will change. Player A will now be the one to get -10 while player B and C will get $10 each. Hence, they will select P(B) and P(C) to be 1/3. Hence, the Nash Equilibrium Dominant Strategy in this case with P(A) = 2/3 is when P(B) = 1/3 and P(C) = 2/3.
Let us now see what happens when P(A) is set to be 6/6 where the probability for the event occurring is high.
Hence, player A will get $10, player B will get -10 and player C will get $10. Hence, they will select P(B) = 3/6 and P(C) = 3/6.
Hence, the Nash Equilibrium Dominant Strategy in this case with P(A) = 6/6 is when P(B) = 3/6 and P(C) = 3/6.
Thus, it can be concluded that the Nash Equilibrium Dominant Strategy in this case will be when P(A) will be 1/3, 2/3, 6/6.
Nash Equilibrium Dominant Strategy in Poker
In Poker, the players have to choose the hand they want to play and also call how much they want to bet. Hence, according to Poker, Nash Equilibrium Dominant Strategy will be when the players make bets that maximize their winnings.
Conclusion
Nash Equilibrium Dominant Strategy is the optimal strategy in a game for an individual or a group when they consider the decisions of others. It is a very important concept in the world of business, economics, and game theory. Hence, learning about Nash Equilibrium Dominant Strategy will help you making sure that you get the best decision possible in any given situation.